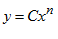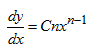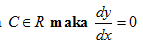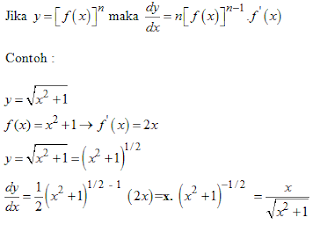1.
Turunan Parsial.
Diketahui z = f(x,y) fungsi dengan dua
variabel independen x dan y. Karena x dan y independen maka :
(i). x
berubah-ubah sedangkan y tertentu.
(ii). y berubah-ubah sedangkan x tertentu.
Definisi
i) Turunan parsial terhadap variabel x
Jika x berubah-ubah dan y
tertentu maka z merupakan fungsi x, Turunan parsial z
= f(x,y) terhadap x sbb :
ii) Turunan parsial
terhadap variabel y
Jika y
berubah-ubah dan x tertentu maka z merupakan fungsi
y, Turunan parsial z
= f(x,y) terhadap y sbb :
a. Fungsi dua peubah atau lebih
Fungsi dua peubah atau lebih dapat
ditulis dalam bentuk eksplisit atau implisit. Jika fungsi dua peubah
dinyatakan dalam bentuk eksplisit, maka secara umum ditulis dalam bentuk z =
F(x,y). Sebaliknya jika fungsi dituliskan dalam bentuk implisit, secara umum
ditulis dalam bentuk F(x,y,z) = 0.
b. Turunan Parsial Fungsi Dua dan Tiga Peubah
Misal z = F(x,y) adalah fungsi dengan variable bebas x dan
y. Karena x dan y variable bebas maka terdapat beberapa kemungkinan yaitu:
1. y dianggap tetap, sedangkan x berubah-ubah
2. x dianggap tetap, sedangkan y berubah-ubah
3. x dan y berubah bersama-sama sekaligus.
Pada kasus 1 dan 2 diatas mengakibatkan fungsinya menjadi
fungsi satu peubah, sehingga fungsi tersebut dapat diturunkan dengan
menggunakan definisi turunan pertama yang telah dipelajari pada kalkulus
diferensial.
Definisi
Misal z = F(x,y) adalah fungsi dua peubah yang terdefinisi
pada interval tertentu, turunan parsial pertama z terhadap x dan y dinotasikan
dengan
dan
Untuk memudahkan persoalan andaikan z = F(x,y) maka untuk menentukan sama artinya dengan menurunkan variabel x dan variabel y dianggap konstan dan selanjutnya y diturunkan. Demikian pula untuk menentukan sama artinya dengan menurukan variable y dan variable x dianggap konstant lalu diturunkan.
Dengan cara yang sama,
andaikan W = F(x,y,z) adalah fungsi tiga peubah yang terdefinisi dalam selang
tertentu maka turunan parsial pertama dinyatakan dengan , dan yang
secara berturut didefinisikan oleh
Asalkan limitnya ada.
Selanjutnya turunan parsial fungsi dua peubah atau
lebih dapat ditentukan turunan parsial ke n, untuk n 2 turunan parsialnya
dinamakan turunan parsial tingkat tinggi.
Dengan menggunakan analogi fungsi satu peubah dapat
ditentukan turunan parsial tingkat 2, 3 dan seterusnya.
CONTOH TURUNAN PARSIAL
1)
Untuk fungsi y = 3x2 – 5z2 + 2x2z –
4xz2 – 9 tentukanlah derivatif parsialnya !
Jawab
:
∂ y =
6x + 4xz – 4z2
∂ x
∂ y =
-10z + 2x2 – 8xz
∂ z
2)
Untuk fungsi y = 3x2 – 5z2 + 2x2z –
4xz2 – 9 tentukanlah diferensial parsialnya !
Jawab
:
∂ y dx
= 6 + 4z
∂ x
∂ y dz
= 4x – 8z
∂ x
∂ y dx
= 4x – 8z
∂ z
∂ y dz
= -10 – 8x
∂ z
2. Total
Diferensial
Diferensial total suatu
fungsi dapat berarti gradien dari fungsi tersebut, yang merupakan jumlah
dari semua diferensial parsial terhadap semua variabel independen.
fungsi-fungsi dengan lebih dari satu variabel
independen
diferensial parsial y terhadap setiap variabel x1 merupakan bagian utama perubahan y yang dihasilkan dari suatu perubahan dx1 dalam variabel tunggal tersebut. Maka, diferensial parsial adalah

melibatkan derivatif parsial y terhadap x1. Jumlah semua diferensial parsial itu terhadap semua variabel independen itulah yang merupakan diferensial total

yang merupakan bagian utama perubahan dalam y sebagai hasil perubahan-perubahan dalam variabel independen xi.
3. Total derivatives
Turunan total fungsi adalah aprokslimasi linear terbaik dari nilai fungsi
 sehubungan dengan argumennya. Tidak seperti derivatif parsial turunan total
mendekati fungsi sehubungan dengan semua argumennya, tidakk hanya satu
pun.Dalam banyak situasi, ini sama dengan mempertimbangkan semua derivatif
parsial secara bersamaan. Istilah
"turunan total" terutama digunakan saat
sehubungan dengan argumennya. Tidak seperti derivatif parsial turunan total
mendekati fungsi sehubungan dengan semua argumennya, tidakk hanya satu
pun.Dalam banyak situasi, ini sama dengan mempertimbangkan semua derivatif
parsial secara bersamaan. Istilah
"turunan total" terutama digunakan saat  adalah fungsi dari beberapa variabel, karena kapan
adalah fungsi dari beberapa variabel, karena kapan  adalah fungsi dari variabel tunggal, turunan total adalah
sama dengan turunan dari fungsi
adalah fungsi dari variabel tunggal, turunan total adalah
sama dengan turunan dari fungsi Ketika fungsi yang sedang dipertimbangkan bernilai nyata, total derivatif dapat disusun kembali menggunakan bentuk diferensial .Misalnya, anggap itu
 adalah fungsi variabel
terdiferensiasi
adalah fungsi variabel
terdiferensiasi  . Total turunan dari
. Total turunan dari  di
di  dapat ditulis dalam bentuk matriks Jacobiannya, yang dalam hal ini
menyederhanakan ke gradien :
dapat ditulis dalam bentuk matriks Jacobiannya, yang dalam hal ini
menyederhanakan ke gradien :
Properti perkiraan linear dari turunan total menyiratkan bahwa jika

adalah vektor kecil (dimana
 menunjukkan
transpose, sehingga vektor ini adalah vektor vektor
kolom), lalu
menunjukkan
transpose, sehingga vektor ini adalah vektor vektor
kolom), lalu
Secara heuristik, ini menunjukkan bahwa jika
 sedikit demi sedikit dalam arah koordinat, kemudian
sedikit demi sedikit dalam arah koordinat, kemudian
Teori bentuk diferensial adalah salah satu cara untuk memberikan arti yang tepat untuk penambahan yang sangat kecil seperti
 . Dalam teori ini,
. Dalam teori ini,  adalah fungsional I
adalah fungsional I
Turunan Parsial Fungsi Implisit
Fungsi Implisit 4 Peubah
BU
dinyatakan dengan

Atau ditulis dalam bentuk
F(x,y,u,v) = 0 dan G(x,y,u,v) = 0
dengan x,y variable berpasangan dan u,v variabel
berpasangan dan F(x,y,u,v) = 0 serta G(x,y,u,v) = 0 tidak dapat berdiri
sendiri.
Untuk menentukan turunan parsial 4 peubah, langkah
ditempuh adalah menurunkan fungsi terhadap peubah yang dimaksud.
Contoh: