A. DEFINISI
Turunan fungsi ( diferensial ) adalah fungsi lain dari suatu fungsi sebelumnya, misal fungsi f menjadi f’ yang mempunyai nilai tidak beratuhan atauTurunan merupakan tingkat perubahan sesaat sebuah fungsi terhadap salah satu variabelnya. Tingkat perubahan fungsi f(x) untuk setiap nilai x, yaitu turunan f(x), dapat dinyatakan dengan rumus:
B. Turunan Fungsi Aljabar
Berikut ini rumus turunan untuk bentuk fungsi aljabar. Rumus ini didapat dari penjabaran rumus turunan di atas.
- Jika y = k, maka y’ = 0
- Jika y = x, maka y’ = 1
- Jika
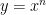 , maka
, maka 
- Jika
 , maka
, maka 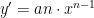
1. Jika 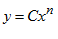 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 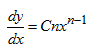

2. Jika y =C dengan 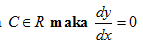

3. Jika y = f(x) + g(x) maka 


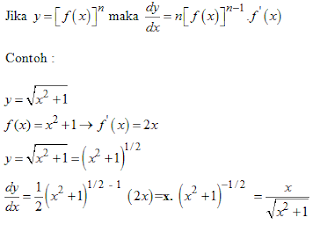
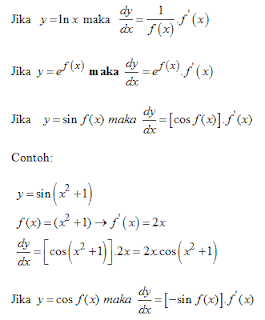
C. Perbedaan
Turunan dan Integral
D. Turunan Trigonometri

1. Jika 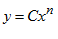 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 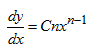
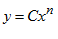 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 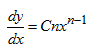
2. Jika y =C dengan
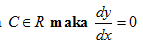
3. Jika y = f(x) + g(x) maka



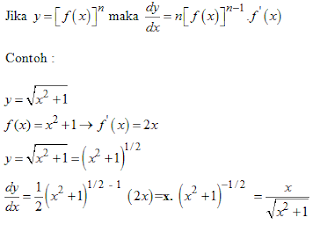
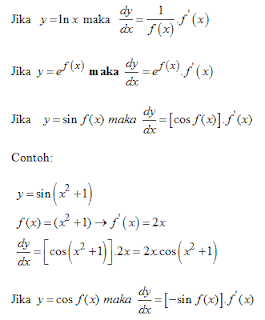
C. Perbedaan
Turunan dan Integral
Turunan
adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai
input, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah
akibat perubahan besaran lainnya. Sedangkan Integral merupakan kebalikan dari
turunan. Jika F(x) adalah fungs umum yang bersifat F(x) = f(x), maka F(x)
merupakan anti turunan atau integral dari f(x).
D. Turunan Trigonometri




Tidak ada komentar:
Posting Komentar