Nama: Ayu Mudmaina
NIM: 20180606032
Agama Islam Seksi 11
Tugas kuliah
Rabu, 10 Juli 2019
Jumat, 05 Juli 2019
Jumat, 28 Desember 2018
INTEGRAL
Pengertian
Integral
Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu. berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral yaitu:
hghg
Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu. berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral yaitu:
hghg
·
Integral sebagai invers/kebalikan dari turunan disebut sebagai
itegral tak tentu.
·
Integral sebagai limit dari jumlah atau suatu luas daerah
tertentudisebut integral tentu.
Rumus
integral f(x)dx
·
f(x) = fungsi yang akan diintegralkan
·
dx = tanda untuk melakukan diferensiasi terhadap x
·
integral f(x)dx sebagai notasi diferensiasi dari the primitive
function/dari fungsi asalnya.
Rumus dasar integral:

INTEGRAL TAK TENTU
Dinamakan integral tak tentu itu karena integral ini tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil
∫ f(x) dx = F(x) + c
INTEGRAL TENTU
Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.

INTEGRAL PARSIAL
Teknik atau metode lain yang bisa digunakan untuk melakukan integral adalah dengan metode parsial. Teknik ini biasanya digunakan untuk mencari suatu fungsi yang tidak dapat dicari integralnya jika menggunakan cara substitusi.
∫ u.dv = u.v – ∫ v. du
INTEGRAL SUBTITUSI
Untuk mengintegralkan sebuah alajabar kita bisa menggunakan metode penggantian atau substitusi. Misalkan u = g(x) dengan g(x) merupkan fungsi yang mempunyai turunan
∫ f(g(x)).g'(x) = ∫ f(u).du = F(u) + c
INTEGRAL FUNGSI ALJABAR
Jika ada fungsi aljabar yang diintegralkan maka sobat bisa menggunakan rumus berikut:

INTEGRAL FUNGSI EKSPONEN

INTEGRAL FUNGSI TRIGONOMETRI
Rumus:
∫ sin x dx = −cos x + C
∫ cos x dx = sin x + C
∫ sec2 x dx = tan x + C
∫ csc2 x dx = −cot x + C
∫ sec x . tan x dx = sec x + C
∫ csc x . cot x dx = −csc x + C
Aturan-Aturan Dasar
Integral
1. Rule 1 (The Power Rule)

2. Rule 2 (The Integral Of Multiple)

3. Rule 3 (The Subtitution Rule)

4. Rule 4 (The Logarithmic Rule)

5. Rule 5 (The Exponential Rule)
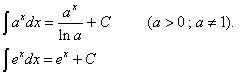
6. Rule 6 (The Integral Of Sum)

7. Rule 7 (Integration by Parts)
Jika u = u(x) dan du = u′(x) dx, sedangkan v = v(x) dan dv = v′(x) dx, lalu integration by parts dinyatakan dengan :
![{\displaystyle {\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&=[u(x)v(x)]_{a}^{b}-\int _{a}^{b}u'(x)v(x)dx\\&=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88aa4b830425c067064d8b5f397f6ea52ed51ada)
atau lebih jelasnya :

8. Rule 8 (Trigonometric Rules)

Contoh :
Rabu, 28 November 2018
MATRIKS
DEFINI
Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang
Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang
Notasi A = (aij)
Artinya
matriks A mempunyai
elemen aij, dimana indeks i menyatakan baris ke-i dan indeks j menyatakan kolom
ke-j dari elemen aij.
Nama matriks menggunakan huruf besar
Elemen atau Anggota atau Unsur menggunakan huruf kecil atau angka
Matriks A = (am x n), ordo matriks A adalah m x n
Nama matriks menggunakan huruf besar
Elemen atau Anggota atau Unsur menggunakan huruf kecil atau angka
Matriks A = (am x n), ordo matriks A adalah m x n
Operasi pada matriks
1. Penjumlahan
Ø Apabila A dan B merupakan dua matriks yang ukurannya sama, maka hasil penjumlahan (A + B) adalah matriks yang diperoleh dengan menambahkan bersama-sama entri yang seletak/bersesuaian dalam kedua matriks tersebut.
Ø Matriks-matriks yang ordo/ukurannya berbeda tidak dapat ditambahkan
2. Pengurangan
Ø Apabila A dan B merupakan dua matriks yang ukurannya sama, maka hasil penguran (A - B) adalah matriks yang diperoleh dengan mengurangi bersama-sama entri yang seletak/bersesuaian dalam kedua matriks tersebut.
Ø Matriks-matriks yang ordo/ukurannya berbeda tidak dapat dikurangkan
3. Perkalian skala dengan matriks
Ø Bila l suatu bilangan dan a = aij maka perkalian l dengan A ditulis A = l(aij) = (laij), atau dengan kata lain matriks lA diperoleh dari perkalian semua elemen A dengan l.
4. Perkalian pada matriks
Ø Bila A = (aij) berordo (pxq)
dan matriks B = (bij) berordo (qxr),
maka perkalian matriks A dan B ditulis AxB,
adalah matriks C = AxB = (cij) berordo (pxr),
dimana cij = a11bij + a12b2j+..….+ a1qbqr
ü Syarat agar matriks A dan B bisa dikalikan adalah banyaknya kolom matriks A harus sama dengan banyaknya baris matriks B.
5. Transpose matriks
Ø Bila matriks A = (aij), berordo (mxn), maka transpose dari matriks A ditulis At adalah matriks yang diperoleh dari A dengan menukar semua baris matriks A menjadi kolom matriks At. Maka matriks At akan berordo nxm.
Jenis-jenis Matriks
Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :
1. Matriks Baris dan Matriks Kolom
Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja. Contoh:
A = (1 4) atau B = (3 7 9) adalah matriks baris
2. Matriks Persegi
Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.
Contoh:
3. Matriks Segitiga Atas dan Segitiga Bawah
Matriks persegi A yang memiliki elemen matriks 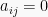 untuk
untuk  atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks
atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks 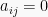 untuk
untuk 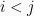 atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
Contoh:
4. Matriks Diagonal
Matriks persegi A yang memiliki elemen matiks 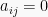 untuk
untuk  atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
Contoh:
5. Matriks Skalar
Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
Contoh:
6. Matriks Indentitas
Matriks diagonal dengan elemen-elemen diagonal utamanya bernilai 1 disebut matriks identitas. Pada umumnya matriks identitas dinotasikan dengan “I”. Contoh:
7. Matriks Simetris
Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen 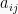 sama dengan elemen
sama dengan elemen 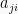 .
.
Contoh:
Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.







Diketahui bahwa P = Q

Contoh soal :
Soal No. 1
Dua buah matriks A dan B masing-masing berturut-turut sebagai berikut:
Dua buah matriks A dan B masing-masing berturut-turut sebagai berikut:

Tentukan A − B
Pembahasan
Operasi pengurangan matriks:
Operasi pengurangan matriks:

Soal No. 2
Dari dua buah matriks yang diberikan di bawah ini,
Dari dua buah matriks yang diberikan di bawah ini,

Tentukan 2A + B
Pembahasan
Mengalikan matriks dengan sebuah bilangan kemudian dilanjutkan dengan penjumlahan:
Mengalikan matriks dengan sebuah bilangan kemudian dilanjutkan dengan penjumlahan:

Soal No. 3
Matriks P dan matriks Q sebagai berikut
Matriks P dan matriks Q sebagai berikut

Tentukan matriks PQ
Pembahasan
Perkalian dua buah matriks
Perkalian dua buah matriks

Soal No. 4
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini

Diketahui bahwa P = Q
Pembahasan
Kesamaan dua buah matriks, terlihat bahwa
Kesamaan dua buah matriks, terlihat bahwa

3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
a + b + x + y = 3 + 5 + 6 + 2 = 16
Selasa, 16 Oktober 2018
TURUNAN FUNGSI 2 VARIABEL
1.
Turunan Parsial.
Diketahui z = f(x,y) fungsi dengan dua
variabel independen x dan y. Karena x dan y independen maka :
(i). x
berubah-ubah sedangkan y tertentu.
(ii). y berubah-ubah sedangkan x tertentu.
Definisi
i) Turunan parsial terhadap variabel x
Jika x berubah-ubah dan y
tertentu maka z merupakan fungsi x, Turunan parsial z
= f(x,y) terhadap x sbb :
ii) Turunan parsial
terhadap variabel y
Jika y
berubah-ubah dan x tertentu maka z merupakan fungsi
y, Turunan parsial z
= f(x,y) terhadap y sbb :
a. Fungsi dua peubah atau lebih
Fungsi dua peubah atau lebih dapat
ditulis dalam bentuk eksplisit atau implisit. Jika fungsi dua peubah
dinyatakan dalam bentuk eksplisit, maka secara umum ditulis dalam bentuk z =
F(x,y). Sebaliknya jika fungsi dituliskan dalam bentuk implisit, secara umum
ditulis dalam bentuk F(x,y,z) = 0.
b. Turunan Parsial Fungsi Dua dan Tiga Peubah
Misal z = F(x,y) adalah fungsi dengan variable bebas x dan
y. Karena x dan y variable bebas maka terdapat beberapa kemungkinan yaitu:
1. y dianggap tetap, sedangkan x berubah-ubah
2. x dianggap tetap, sedangkan y berubah-ubah
3. x dan y berubah bersama-sama sekaligus.
Pada kasus 1 dan 2 diatas mengakibatkan fungsinya menjadi
fungsi satu peubah, sehingga fungsi tersebut dapat diturunkan dengan
menggunakan definisi turunan pertama yang telah dipelajari pada kalkulus
diferensial.
Definisi
Misal z = F(x,y) adalah fungsi dua peubah yang terdefinisi
pada interval tertentu, turunan parsial pertama z terhadap x dan y dinotasikan
dengan
dan
Untuk memudahkan persoalan andaikan z = F(x,y) maka untuk menentukan sama artinya dengan menurunkan variabel x dan variabel y dianggap konstan dan selanjutnya y diturunkan. Demikian pula untuk menentukan sama artinya dengan menurukan variable y dan variable x dianggap konstant lalu diturunkan.
Dengan cara yang sama,
andaikan W = F(x,y,z) adalah fungsi tiga peubah yang terdefinisi dalam selang
tertentu maka turunan parsial pertama dinyatakan dengan , dan yang
secara berturut didefinisikan oleh
Asalkan limitnya ada.
Selanjutnya turunan parsial fungsi dua peubah atau
lebih dapat ditentukan turunan parsial ke n, untuk n 2 turunan parsialnya
dinamakan turunan parsial tingkat tinggi.
Dengan menggunakan analogi fungsi satu peubah dapat
ditentukan turunan parsial tingkat 2, 3 dan seterusnya.
CONTOH TURUNAN PARSIAL
1)
Untuk fungsi y = 3x2 – 5z2 + 2x2z –
4xz2 – 9 tentukanlah derivatif parsialnya !
Jawab
:
∂ y =
6x + 4xz – 4z2
∂ x
∂ y =
-10z + 2x2 – 8xz
∂ z
2)
Untuk fungsi y = 3x2 – 5z2 + 2x2z –
4xz2 – 9 tentukanlah diferensial parsialnya !
Jawab
:
∂ y dx
= 6 + 4z
∂ x
∂ y dz
= 4x – 8z
∂ x
∂ y dx
= 4x – 8z
∂ z
∂ y dz
= -10 – 8x
∂ z
2. Total
Diferensial
Diferensial total suatu
fungsi dapat berarti gradien dari fungsi tersebut, yang merupakan jumlah
dari semua diferensial parsial terhadap semua variabel independen.
fungsi-fungsi dengan lebih dari satu variabel
independen
diferensial parsial y terhadap setiap variabel x1 merupakan bagian utama perubahan y yang dihasilkan dari suatu perubahan dx1 dalam variabel tunggal tersebut. Maka, diferensial parsial adalah

melibatkan derivatif parsial y terhadap x1. Jumlah semua diferensial parsial itu terhadap semua variabel independen itulah yang merupakan diferensial total

yang merupakan bagian utama perubahan dalam y sebagai hasil perubahan-perubahan dalam variabel independen xi.
3. Total derivatives
Turunan total fungsi adalah aprokslimasi linear terbaik dari nilai fungsi
 sehubungan dengan argumennya. Tidak seperti derivatif parsial turunan total
mendekati fungsi sehubungan dengan semua argumennya, tidakk hanya satu
pun.Dalam banyak situasi, ini sama dengan mempertimbangkan semua derivatif
parsial secara bersamaan. Istilah
"turunan total" terutama digunakan saat
sehubungan dengan argumennya. Tidak seperti derivatif parsial turunan total
mendekati fungsi sehubungan dengan semua argumennya, tidakk hanya satu
pun.Dalam banyak situasi, ini sama dengan mempertimbangkan semua derivatif
parsial secara bersamaan. Istilah
"turunan total" terutama digunakan saat  adalah fungsi dari beberapa variabel, karena kapan
adalah fungsi dari beberapa variabel, karena kapan  adalah fungsi dari variabel tunggal, turunan total adalah
sama dengan turunan dari fungsi
adalah fungsi dari variabel tunggal, turunan total adalah
sama dengan turunan dari fungsi Ketika fungsi yang sedang dipertimbangkan bernilai nyata, total derivatif dapat disusun kembali menggunakan bentuk diferensial .Misalnya, anggap itu
 adalah fungsi variabel
terdiferensiasi
adalah fungsi variabel
terdiferensiasi  . Total turunan dari
. Total turunan dari  di
di  dapat ditulis dalam bentuk matriks Jacobiannya, yang dalam hal ini
menyederhanakan ke gradien :
dapat ditulis dalam bentuk matriks Jacobiannya, yang dalam hal ini
menyederhanakan ke gradien :
Properti perkiraan linear dari turunan total menyiratkan bahwa jika

adalah vektor kecil (dimana
 menunjukkan
transpose, sehingga vektor ini adalah vektor vektor
kolom), lalu
menunjukkan
transpose, sehingga vektor ini adalah vektor vektor
kolom), lalu
Secara heuristik, ini menunjukkan bahwa jika
 sedikit demi sedikit dalam arah koordinat, kemudian
sedikit demi sedikit dalam arah koordinat, kemudian
Teori bentuk diferensial adalah salah satu cara untuk memberikan arti yang tepat untuk penambahan yang sangat kecil seperti
 . Dalam teori ini,
. Dalam teori ini,  adalah fungsional I
adalah fungsional I
Turunan Parsial Fungsi Implisit
Fungsi Implisit 4 Peubah
BU
dinyatakan dengan

Atau ditulis dalam bentuk
F(x,y,u,v) = 0 dan G(x,y,u,v) = 0
dengan x,y variable berpasangan dan u,v variabel
berpasangan dan F(x,y,u,v) = 0 serta G(x,y,u,v) = 0 tidak dapat berdiri
sendiri.
Untuk menentukan turunan parsial 4 peubah, langkah
ditempuh adalah menurunkan fungsi terhadap peubah yang dimaksud.
Contoh:


Langganan:
Postingan (Atom)
Tugas PAI Sesi 11
Nama: Ayu Mudmaina NIM: 20180606032 Agama Islam Seksi 11
-
RELASI PENGERTIAN RELASI Relasi adalah suatu aturan yang memasangkan anggota himpunan ke himpunan lain. Suatu relasi dari himpunan A k...
-
Pengertian Integral Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari juml...
-
A. DEFINISI Turunan fungsi ( diferensial ) adalah fungsi lain dari suatu fungsi sebelumnya, misal fungsi f menjadi f’ yang mempuny...

