DEFINI
Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang
Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang
Notasi A = (aij)
Artinya
matriks A mempunyai
elemen aij, dimana indeks i menyatakan baris ke-i dan indeks j menyatakan kolom
ke-j dari elemen aij.
Nama matriks menggunakan huruf besar
Elemen atau Anggota atau Unsur menggunakan huruf kecil atau angka
Matriks A = (am x n), ordo matriks A adalah m x n
Nama matriks menggunakan huruf besar
Elemen atau Anggota atau Unsur menggunakan huruf kecil atau angka
Matriks A = (am x n), ordo matriks A adalah m x n
Operasi pada matriks
1. Penjumlahan
Ø Apabila A dan B merupakan dua matriks yang ukurannya sama, maka hasil penjumlahan (A + B) adalah matriks yang diperoleh dengan menambahkan bersama-sama entri yang seletak/bersesuaian dalam kedua matriks tersebut.
Ø Matriks-matriks yang ordo/ukurannya berbeda tidak dapat ditambahkan
2. Pengurangan
Ø Apabila A dan B merupakan dua matriks yang ukurannya sama, maka hasil penguran (A - B) adalah matriks yang diperoleh dengan mengurangi bersama-sama entri yang seletak/bersesuaian dalam kedua matriks tersebut.
Ø Matriks-matriks yang ordo/ukurannya berbeda tidak dapat dikurangkan
3. Perkalian skala dengan matriks
Ø Bila l suatu bilangan dan a = aij maka perkalian l dengan A ditulis A = l(aij) = (laij), atau dengan kata lain matriks lA diperoleh dari perkalian semua elemen A dengan l.
4. Perkalian pada matriks
Ø Bila A = (aij) berordo (pxq)
dan matriks B = (bij) berordo (qxr),
maka perkalian matriks A dan B ditulis AxB,
adalah matriks C = AxB = (cij) berordo (pxr),
dimana cij = a11bij + a12b2j+..….+ a1qbqr
ü Syarat agar matriks A dan B bisa dikalikan adalah banyaknya kolom matriks A harus sama dengan banyaknya baris matriks B.
5. Transpose matriks
Ø Bila matriks A = (aij), berordo (mxn), maka transpose dari matriks A ditulis At adalah matriks yang diperoleh dari A dengan menukar semua baris matriks A menjadi kolom matriks At. Maka matriks At akan berordo nxm.
Jenis-jenis Matriks
Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :
1. Matriks Baris dan Matriks Kolom
Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja. Contoh:
A = (1 4) atau B = (3 7 9) adalah matriks baris
2. Matriks Persegi
Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.
Contoh:
3. Matriks Segitiga Atas dan Segitiga Bawah
Matriks persegi A yang memiliki elemen matriks 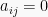 untuk
untuk  atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks
atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks 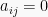 untuk
untuk 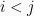 atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
Contoh:
4. Matriks Diagonal
Matriks persegi A yang memiliki elemen matiks 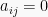 untuk
untuk  atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
Contoh:
5. Matriks Skalar
Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
Contoh:
6. Matriks Indentitas
Matriks diagonal dengan elemen-elemen diagonal utamanya bernilai 1 disebut matriks identitas. Pada umumnya matriks identitas dinotasikan dengan “I”. Contoh:
7. Matriks Simetris
Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen 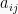 sama dengan elemen
sama dengan elemen 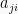 .
.
Contoh:
Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.







Diketahui bahwa P = Q

Contoh soal :
Soal No. 1
Dua buah matriks A dan B masing-masing berturut-turut sebagai berikut:
Dua buah matriks A dan B masing-masing berturut-turut sebagai berikut:

Tentukan A − B
Pembahasan
Operasi pengurangan matriks:
Operasi pengurangan matriks:

Soal No. 2
Dari dua buah matriks yang diberikan di bawah ini,
Dari dua buah matriks yang diberikan di bawah ini,

Tentukan 2A + B
Pembahasan
Mengalikan matriks dengan sebuah bilangan kemudian dilanjutkan dengan penjumlahan:
Mengalikan matriks dengan sebuah bilangan kemudian dilanjutkan dengan penjumlahan:

Soal No. 3
Matriks P dan matriks Q sebagai berikut
Matriks P dan matriks Q sebagai berikut

Tentukan matriks PQ
Pembahasan
Perkalian dua buah matriks
Perkalian dua buah matriks

Soal No. 4
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini

Diketahui bahwa P = Q
Pembahasan
Kesamaan dua buah matriks, terlihat bahwa
Kesamaan dua buah matriks, terlihat bahwa

3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
a + b + x + y = 3 + 5 + 6 + 2 = 16
